《Computer Systems A Programmers perspective》第2章习题
深入理解计算机系统.第二章习题记录

A. 通过展开每个十六进制转换为二进制:
2 5 B 9 D 2
0010 0101 1011 1001 1101 0010
b. 先分为4位一组, 不足四位的, 前边补零:> 1010 1110 0100 1001
A E 4 9
c. 同 A
A 8 B 3 D
1010 1000 1011 0011 1101
d. 同b
0011 0010 0010 1101 1001 0110
3 2 2 D 9 5

仅关注hex, 则有 23=3+4*5=0x800000,
2^15=32768, 15=3+4*2=0x800,
0x2000=1+4*3=2^13,
12=4*3+0=0x1000,
64=2^6=4*1+2=0x20,
0x100=64

十进制与十六进制之间的转换相对更容易些, 如下:
158=16*9 + 14 = 0x9E = 1001 1110
76=16*4 + 12 = 0x4C = 0100 1100
145=16*9 + 1 = 0x91 = 1001 0001
1010 1110 = 0xAE = 16 * 10 + 14 = 174
0011 1100 = 0x3C = 16*3 + 12 = 60
1111 0001 = 0xF1 = 16*15 + 1 = 241

在某个数大于15时才发生进位. 如果减完小于0时, 则变成F即可: A. 0x6061 B. 0x603c C. 0x608e D. 0x009e

小端即尾部在前, 大端即头部在前
A. 78 | 12
B. 78 56 | 12 34
C. 78 56 34 | 12 34 56

A. 0027C8F8 -> 0010 0111 1100 1000 1111 1000
4A1F23E0 -> 0100 1010 0001 1111 0010 0011 1110 0000
B.0 0111 1100 1000 1111 1000 共21位能匹配上
C. 整形表示的前几位以及浮点的前后几位对不上

由于字符编码方式是固定从前到后, 且在尾部填充0x00, 所以打印的结果为: 6D 6E 6F 70 71 72

~a 10110001
~b 00011110
a&b 01000000
a|b 11101111
a^b 10010000
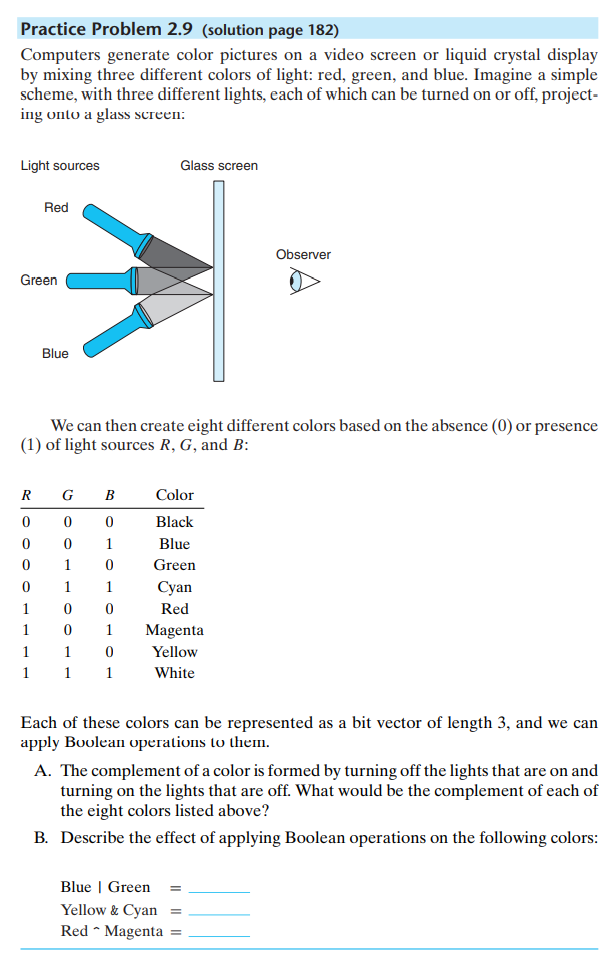
A. Black <> White
Blue <> Yellow
Green <> Magenta
Cyan <> Red
B. 001 | 010 = 011 = Cyan
110 & 011 = 010 = Green
100 ^ 101 = 001 = Blue

Step 1 : a a^b
Step 2 : 0^b=b a^b
Step 3 : b a

A. 循环到结尾时, 头指针与尾指针是指向同一个元素的, 就是k;
B. 因为inplace_swap第一步就是对输入的两个参数进行异或,自身与自身异或后就变成0;
C. 将first<=last改为first<last即可避免该问题。

A. x & 0xFF
B. x ^ ~0xFF
C. x | 0xFF

首先写出bis与bic的C语言形式如下:
bis -> x | m
bic -> x & ~m
现在要求x | y 则直接调用bis即可 bis(x, y)
要求 x ^ y 等效于找到一个掩码m, 这个码在x与y相同的位上为1,不同的位上为0,然后用bis和bic配合达到异或效果。
某一位上 xy 同时为1, 则bis为1, bic为0; xy同时为0则bis为0, bic为0; x为1 y为0则bis为1, bic为1, x为0 y为1则bis为1, bic为0
调用两次bic再对结果bis即可:
bis(bic(x,y), bic(y,x))

0x55 = 0101 0101 0x46 = 0100 0110
~0x55 = 1010 1010 ~0x46 = 1011 1001
a&b = 0100 0100 a&&b = true
a|b = 0101 0111 a||b = true
~a|~b = 1011 1011 !a||!b = false
a&!b = 0001 0001 a&&~b = false

思路:通过异或可以实现在x等于y时结果为0,其余情况下均不为0,然后取反即可。
!(x ^ y)

0xD4 = 1101 0100 <<2 0101 0000 >>>3 0001 1010 >>3 1111 1010
0x64 = 0110 0100 <<2 1001 0000 >>>3 0000 1100 >>3 0000 1100
0x72 = 0111 0010 <<2 1100 1000 >>>3 0000 1110 >>3 0000 1110
0x44 = 0100 0100 <<2 0001 0000 >>>3 0000 1000 >>3 0000 1000

0x1 = 0001 = 2^0 = 1 = 1
0xB = 1011 = 2^3 + 2^1 + 2^0 = 11 = -5
0x2 = 0010 = 2^1 = 2 = 2
0x7 = 0111 = 2^2 + 2^1 + 2^0 = 7 = 7
0xC = 1100 = 2^3 + 2^2 = 12 = -4
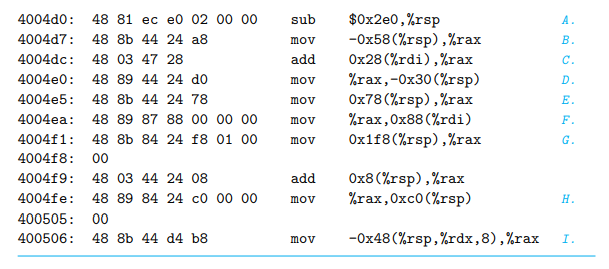
32位补码形式表示的十六进制 -> 等价的十进制
此题意思不明确,跳过。

T2U表示将有符号数转化为无符号数:
-1 1111 > 15
-5 1011 > 11
-6 1010 > 10
-4 1010 > 12
1 0001 > 1
8 有bug,无法表示

答: 对于-1、-5、-6与-4,由于是负数需要加上2^4=16. 对于1保持不变即可。

无符号 0
有符号 1
无符号 0
有符号 1
无符号 1

A. 套用B2T的公式得到 -1 * 2^3 + 2 + 1 = -5
B. 根据符号扩展可得 11011=1011
C. 同B.
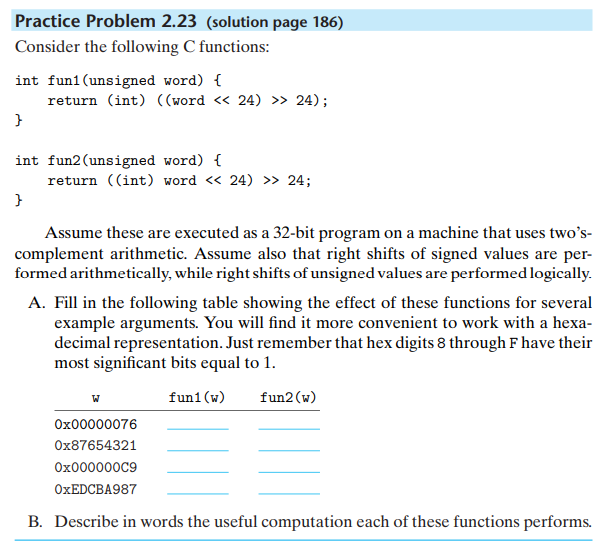
A. word是无符号型, 所以直接对word做移位都是逻辑移位. 同时unsigned是32位的, 相当于8个十六进制数字, 移24位相当于6个十六进制.
强制类型转换的优先级要高于移位的优先级. 强制类型转换会保持位模式不变, 但是移位后变成算数移位.
0x00000076 0x00000076
0x00000021 0x00000021
0x000000C9 0xFFFFFFC9
0x00000087 0xFFFFFF87
B.
func1 转为int型并保留最后两位数字
func2 在最后两位小于0x80时取原始值;大于等于0x80时取补码值;?
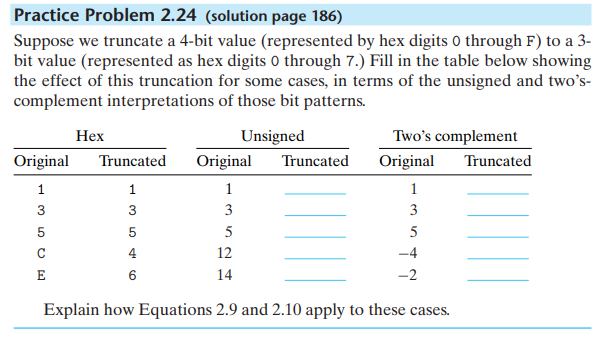
无符号数截断直接移除首位即可:
0001 = 001 = 1
0011 = 011 = 3
1100 = 100 = 4
1110 = 110 = 6
有符号数也是移除首位, 不过按照有符号来计算实际值:
1
3
-4
-2

在表达式中同时包含有符号和无符号数时, 会将所有数字都转为无符号数再进行计算. 因此
length - 1 变为 0U - 1U (这是无符号运算) 值为 2^32 -1. 导致 result += a[1]会被执行, 出现错误. 可以修改为:
for (i=0; i < length; i++)

A. 在s的长度小于t的长度时会发生此种情况.
B. 因为无符号数减法, 如果s<t则会出现溢出, 导致结果是一个很大的正数.
C> 改为strlen(s) > strlen(t)即可

int uadd_ok(unsigned x, unsigned y){
if (x + y >= x) {
return 1;
} else {
return 0;
}
}
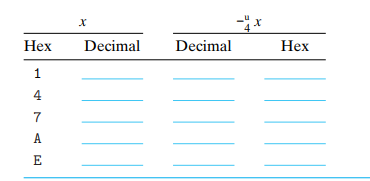
1 = 1 > 2^4 - 1 = 15 = F 0001 <> 1111
4 = 4 > 2^4 - 4 = 12 = C
7 = 7 > 2^4 - 7 = 9 = 9
A = 10 > 2^4 - 10 = 6 = 6
E = 14 > 2^4 - 14 = 2 = 2
2 = 2 > 2^4 -2 = 14 = E 0010 <> 1110
9 = 9 > 2^4 -9 = 7 1001 <> 0111

10100 + 10001 ( -12 + -15 = -27 ) == 00101 = 5 > situation 1
11000 + 11000 ( -8 + -8 = -16 ) == 10000 = -16 > situation 2
10111 + 01000 ( -9 + 8 = -1 ) == 11111 = -1 > situation 2
00010 + 00101 ( 2 + 5 = 7 ) == 00111 = 7 > situation 3
01100 + 00100 ( 12 + 4 = 16 ) == 10000 = -16 > situation 4

int tadd_ok(int x, int y){
if (x<0 && y<0 && x + y >= 0) {
return 0;
} else if (x>0 && y>0 && x + y <=0) {
return 0;
} else {
return 1;
}
}

由于补码的加减法在位表示上与无符号数完全相同, 因此先加后减并不会损失信息, 因此该函数的返回结果恒为真.

注意到y的取值范围是-2^32 ~ 2^32-1. 当y取-2^32时, 直接-y就必然会产生溢出. 此时x是任意非负值, 都会导致结果不对.
为了修复这个问题, 可以同时判断y-x也不会发生溢出. 因为如果x-y溢出了, 那么y-x肯定也溢出了.
int tsub_ok(int x, int y){
return tadd_ok(x, -y) && tadd_ok(y, -x);
}

2H = 2D -2H = -2D 0010 <> 1110
3H = 3D -3H = -3D
9H = 1001 = -7D -9H = 7D 0111
BH = 1011 = -5D -BH = 5D 0101
CH = 1100 = -4D -CH = 4D 0100
两者的位模式完全相同, 因为他们都要求加和为0. 因此我们可以用unsigned的逆元来求signed的逆元.

无符号: x=100B=4D y=101B=5D x*y=20D=10100 截断后为100
补码: x=100B=-4D y=101B=-3D x*y=12D=01100 截断后为100

- argue that the case x=0 is handled correctly.
0乘任何数都为0, 一定不可能溢出, 所以x=0时必然返回1, 是正确的.
- 证明 x*y=p+t2^w
xy的结果只有两种, 溢出或者不溢出. 溢出时, 结果位数大于w小于等于2w, 将结果拆分为w+1位-2w位和1-w位两部分.分别对应于s和p.s可以看做是一个不超过w位的数移位w位得到, 即s=t2^w. 当且仅当t不为0时, s不为0, xy发生溢出.
- 证明p可以写作p=x*q+r
由于p就是x/q的结果, 所以p=x*q加上余数, 余数r的绝对值小于x
- 证明当且仅当r=t=0时, q=y
证明if: 如果r=t=0 根据公式可得xy=xq, 又因为x不为0, 所以y=q
证明onlyif: 如果r或者t中任意一个不为0, 则xy=xq+N, N不为0, 此时y=(q+N/x)不等于q.

// 如果溢出, 则32~64位必不为0
int tmult_ok(int x, int y) {
int64_t p = (int64_t)x * y; // 注意此处必需先做强制类型转换, 否则结果会变为溢出之后的结果
return (int)p == p; // 用移位的话, 负数可能会有问题
}

k=0 b=0 1倍 b=a 2倍
k=1 b=0 2倍 b=a 3倍
k=2 b=0 4倍 b=a 5倍
k=3 b=0 8倍 b=a 9倍

可以修改为 x<<n + x<<n - x<<m

K = 7 移位1次, 由于7=8-1, 所以使用 x<<3 - x即可
K = 30 = 11110, 移位4次, 和有效位数量相同, 因此使用 x<<4 + x<<3 + x<<2 + x<<1即可
K = 28 = 11100, 移位2次, 28=100000 - 100, 因此使用 x<<5 - x<<2即可
K = 55 = 110111, 移位2次, 加减两次. 我们先将K+1可以得到111000, 这个可以用两次移位和一次加减得到即 x<<6-x<<3, 然后再减去加的一次得到 x<<6-x<<3-x即可

在n=m时, 使用A. n!=m时, 由于加法和减法的开销相同, 因此优先使用B. 如B会造成溢出, 再使用A.

int div16(x)
{
int symbol_bit = x>>32 & 1;
return x + (symbol_bit<<4 - symbol_bit) >> 4;
}

将optarith写成数学表达式, 我们可以得到:
x * 32 - x + y/8
所以M=31, N=8

A. 2 x=-2^32时, x-1>0 且x<0
B. 1 7 = 111, x<<29为左移不用考虑符号位?
C. 2 x>2^16次方会产生溢出
D. 2 x不为-2^32
E. 这个题目肯定有问题
F. 2 任意两个相加不会溢出的负数, 如-1和-1
G. 2 假设x,y均大于0, 则 x*~y + uy*ux = x*~y + y*x=x*(y+~y), 不成立
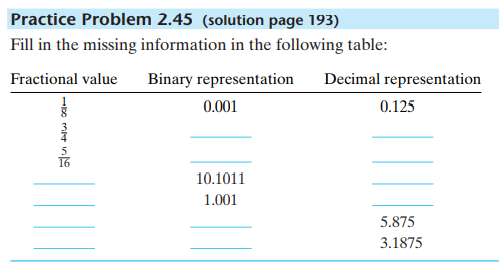
3/4 = 0.11B = 0.75D
5/16 = 0.0101B = 0.3125D
10.1011 = 2 + 1/2 + 1/8 + 1/16 = 43/16 = 2.6875D
1.001 = 1 + 1/8 = 9/8 = 1.125D
5.875 = 5875/1000 = 47/8 = 101.111B
3.1875 = 31875/10000 = 255/80 = 51/16 = 11.0011B

A. 0.000000000000000000000[0011]...
B. x = 3/32 + 3/512 + 3/8192 + 3/131072 + 3/2097152 = 0.099999904632 0.1-x = 0.000000093 = 9*10^-8
C. 100h = 100 3600s = 0.3610^6, 100h 910^-8 = 3.24*10^-2
D, 3.2410^-2 2000 = 62.8m
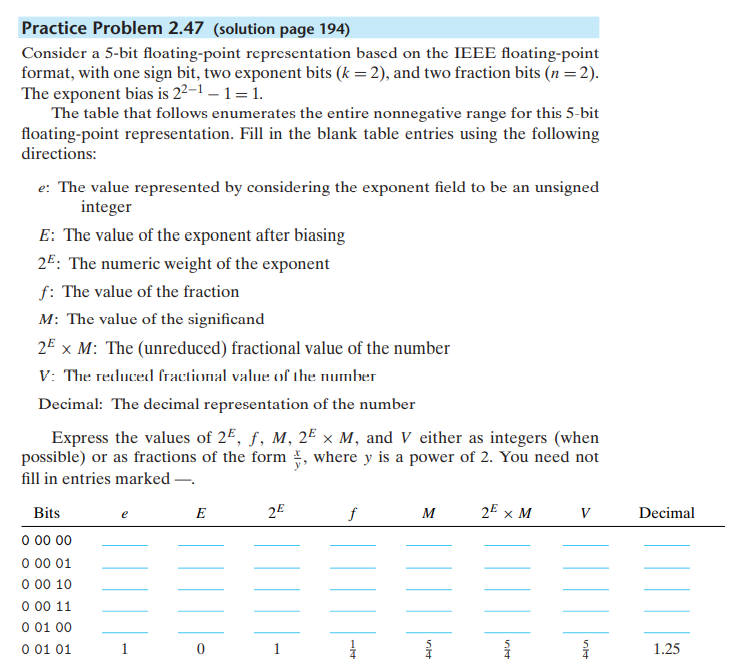
在阶码为全0时, 阶码偏置后为1-Bias,这里Bias为1所以偏置后为0, 此时f没有隐含的1就是原始小数:
0 00 00 e=0 E=0 2^E=1 f=0 M=0 2^E*M = 0 V=+0 Dec=0
0 00 01 e=0 E=0 2^E=1 f=1/4 M=1/4 2^E*M=1/4 V=1/4 Dec=0.25
0 00 10 e=0 E=0 2^E=1 f=2/4 M=2/4 2^E*M=1/4 V=1/2 Dec=0.5
0 00 10 e=0 E=0 2^E=1 f=3/4 M=3/4 2^E*M=3/4 V=3/4 Dec=0.75
0 01 00 e=1 E=0 2^E=1 f=4/4 M=4/4 2^E*M=4/4 V=1 Dec=1

3510593 = 11 0101 1001 0001 0100 0001B
32位包括1个符号位,8个阶码位与23个小数位。
阶码偏置为127,E=e-127. 由于3510593一共是22位,刨除一个隐含位,剩余21位,需要左移21位可以得到阶码为148,转化为二进制为10010100.
因此全部位为
0100 1010 0101 0110 0100 0101 0000 0100 即4A564504

A.不能准确描述的最小正整数 - 相当于无论如何左移或者右移均达不到要求。考虑到隐含位,此时该整数的最高位一定是1.同时,如果该整数是在n+1位以内, 那么都可以表示。包括首位为0余下都为1的情形,这时只需要在尾部留一个0然后控制阶数即可。因此该整数一定是n+2位,首位为1,且末位不为0,满足该条件最小的数为2^(n+1)+1
B.2^24+1=16777217

A. 不是在中间,所以舍入为11.0
B. 在中间, 舍入偶数为11.0
C. 不在中间, 舍入为11.0
D. 在中间,舍入为11.0

A. 0.0001 1001 1001 1001 1001 [1001] 由于尾部为110>100, 所以舍入后为 0.0001 1001 1001 1001 1001 101
B. 约为0.0000002384185791015625=2.384*10^-8
C. 约为8.58*10^-3
D. 约为1.72m
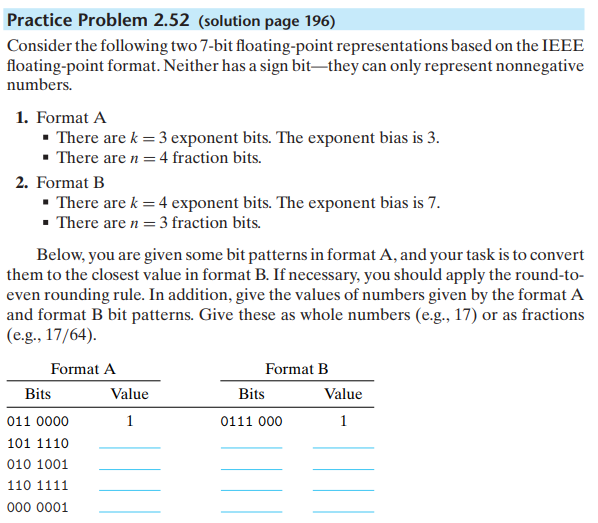
101 1110 > 2^2 * 1.111=111.1=15/2 由于有4位小数,需要舍入,舍入后为1000 = 2^3, 3+7=10所以E=1010, 1010 000
010 1001 > 1/2 * 1.1001=0.11001=1/2+1/4+1/32=25/32, 由于有5位小数,需要舍入,舍入后为0.1100, 移位-1,-1+7=6所以E=0110, 0110 100
110 1111 > 2^3 * 1.1111=1111.1=31/2, 由于有5位小数, 需要舍入, 舍入后为10000, 移位4, 4+7=13所以E=1101, 1101 000
000 0001 > 2^-2 * 0.0001 = 0.000001=1/64, 用非规则形式, E=1-7=-6, 无法表示。用规则形式,隐含位移-6位,-6+7=1所以E=0001, 0001 000


A. 总是为真。 因为int转double能保留精确值,double转int在范围内
B. 不总是为真,可能发生舍入。如2^24+1就会有问题。
C. 不总是为真,同上;
D. ~不总是为真,同上;~ 同A.
E. ~不总是为真, f=-2^32时,-f=0, -0仍然为0.~ float型只需要改变符号位即可