Pytorch一小时入门
抄写一遍Pytorch入门代码
更新记录:
20/05/31(I) 完成前两节(30min)的内容
20/05/31(II) 完成后两节(30min)的内容
学习了DEEP LEARNING WITH PYTORCH: A 60 MINUTE BLITZ,将过程记录在此处。

- 1.理解PyTorch的Tensor库
- 2.Autograd自动求导的应用
- 3.构建神经网络
- 4.一个实际的例子
from __future__ import print_function
import torch
# check the GPU support
dir(torch.cuda)
assert(torch.cuda.is_available())
创建一个5x3张量,不初始化
x=torch.empty(5,3)
print(x)
???这里的表现和页面不一样,预期应该是全0才对
创建一个随机初始化张量
x=torch.rand(5,3)
print(x)
创建一个填0的long型张量
x=torch.zeros(5,3,dtype=torch.long)
print(x)
从数据中直接创建一个张量
x=torch.tensor([5.5,3.0])
print(x)
根据一个已有张量创建张量
# 创建一个类型变为double型的全1张量
x=x.new_ones(5,3,dtype=torch.double)
print(x)
x=torch.randn_like(x,dtype=torch.float)
print(x)
torch.size实际是一个tuple
print(x.size())
print(x.size()[0])
加法之两种符号类型
# 类型1- 直接用加号
x = torch.ones(5,3)
y = torch.zeros(5,3)
print(x + y)
# 类型2- 使用函数add
print(torch.add(x,y))
???为何要用两种符号表示呢
加法之指定结果tensor
result = torch.empty(5,3)
torch.add(x,y,out=result)
print(result)
加法之原位相加
y.add_(x)
print(y)
注意到所有原位运算都是在函数名后边加一个下划线
使用类似numpy的范围写法取tensor的部分值
# 打印x的第一列
print(x[:,1])
# 打印x的第一行
print(x[1,:])
改变tensor的维度
x = torch.randn(4,4)
y = x.view(16)
# 只指定每行的元素数量,就可以计算出变换后的形状
z = x.view(-1, 2)
print(x,y,z)
tensor的操作还有很多,此处实际没有完全列举
numpy数组和tensor共享内存:这意味着对任何一个变量的改变都将同步到另一个上。
转化tensor为一个ndarray
a=torch.ones(5)
b=a.numpy()
print(a,b)
对tensor的改变将会反映到ndarray上
a.add_(a)
print(b)
对ndarray的改变将会反映到tensor上
b+=1
print(a)
将ndarray转换为tensor
import numpy as np
a = np.ones(5) #注意此处的变量命名
b = torch.from_numpy(a)
np.add(a,1,out=a)
print(a)
print(b)
使用to()方法将tensor迁移到其它设备
device = torch.device("cuda")
y = torch.ones_like(x, device=device)
x = x.to(device)
z = x + y
print(z)
print(z.to("cpu", torch.int))
pytorch中神经网络的核心模块就是autograd包,我们简单地了解一下这个包,其后就可以开始训练我们的第一个神经网络了。
autograd包可以对所有的tensor操作进行自动差分(???如何自定义运算符)。它是一个define-by-run的框架,也就是你的反向传播是由代码运行方式所决定的,每一个操作都会有不同。
我们用更简单的方式和例子进行解释。
tensor
torch.Tensor是这个包的核心。如果你将其属性.requires_grad设为True,它将追踪其上的所有操作。当你完成计算后,可以调用.backward()方法以自动计算所有导数。这个tensor的导数将由.grad参数所体现。
为了结束对一个tensor求导的操作,你可以用.detach方法将它从计算历史中移除,以避免之后它又被继续求导。
为了避免对tensor求导占用内存,你可以将代码块用with torch.no_grad()包裹起来。这对模型评估尤其有用,因为其中可能存在设置了require_grad=True的参数,但我们却不需要求导数。
Function类是另外一个非常常用的类。
Tensor和Function共同作用以构建一个无环图,该图对完整的计算历史进行编码。每个tensor都有一个.grad_fn属性,其中保存了创建这个tensor的Function对象。(用户自己创建的tensor则没有这个属性)
如果你想计算导数,你可以调用tensor的.backward()方法。如果tensor是一个标量(即包含单个元素),你不需要为backward()指定任何参数。但如果它有多于一个元素,则你必需为它指定gradient参数,其形状与该tensor对应。
创建一个tensor并设定
require_grad为True以追踪其上的计算:
x = torch.ones(2,2,requires_grad=True)
print(x)
tensor运算
y = x + 2
print(y)
更多的tensor运算
z = y * y * 3
out = z.mean()
print(z, out)
.requires_grad_()可用于替换一个已有tensor的require_grad标志位。输入标志位默认为False。
a = torch.randn(2,2)
a=((a*3)/(a-1))
print(a.requires_grad)
print(a.grad_fn)
a.requires_grad_(True)
print(a.requires_grad)
print(a.grad_fn)
b=(a*a).sum()
print(b.grad_fn)
进行反向传播。由于
out是一个标量,所以无需传入参数
out.backward()
print(x.grad)
如果我们将out定义为$o$,那么我们将有$o=\frac{1}{4}\sum_{i}3(x_i+2)^2$,此时$\frac{\partial o}{\partial x_i}=\frac{3}{2}(x_i+2)$,因此$\frac{\partial o}{\partial x_i} \mid_{x_i=1}=4.5$
数学上来说,如果你有一个因自变量都为向量的函数$\vec{y}=f(\vec{x})$,那么$\vec{y}$对$\vec{x}$的导数为一个雅可比矩阵:
$J=\left(\begin{array}{ccc} \frac{\partial y_{1}}{\partial x_{1}} & \cdots & \frac{\partial y_{1}}{\partial x_{n}} \\ \vdots & \ddots & \vdots \\ \frac{\partial y_{m}}{\partial x_{1}} & \cdots & \frac{\partial y_{m}}{\partial x_{n}} \end{array}\right)$
一般地,torch.autograd是一个用于计算向量-雅可比行列式乘积的工具。也就是说,给定任何向量$v=(v_1 v_2 ... v_m)^T$,如果$v$刚好是标量函数$l=g(\vec{y})$的导数,也就是说$v=\left(\frac{\partial l}{\partial y_{1}} \cdots \frac{\partial l}{\partial y_{m}}\right)^{T}$,那么根据链式法则有向量与雅克比行列式之积为
$J^{T} \cdot v=\left(\begin{array}{ccc}
\frac{\partial y_{1}}{\partial x_{1}} & \cdots & \frac{\partial y_{m}}{\partial x_{1}} \\
\vdots & \ddots & \vdots \\
\frac{\partial y_{1}}{\partial x_{n}} & \cdots & \frac{\partial y_{m}}{\partial x_{n}}
\end{array}\right)\left(\begin{array}{c}
\frac{\partial l}{\partial y_{1}} \\
\frac{\partial l}{\partial y_{m}}
\end{array}\right)=\left(\begin{array}{c}
\frac{\partial l}{\partial x_{1}} \\
\frac{\partial l}{\partial x_{n}}
\end{array}\right)$
向量与雅克比行列式之积的这种性质使得,将额外的导数引入输出不为常量的模型非常方便。 现在我们看一下向量-雅克比积的一个例子:
x = torch.randn(3, requires_grad=True)
y = x * 2
while y.data.norm()<1000:
y=y*2
print(y)
在这个例子中y不再是一个标量了。torch.autograd不能直接计算完整的雅克比行列式,但如果我们只想要向量-雅克比行列式之积的话,就简单将向量传入backward参数即可:
v = torch.tensor([0.1,1.0,0.0001], dtype=torch.float)
y.backward(v)
print(x.grad)
关于上面这一段知乎链接讲的比较清楚,主要动机是不允许tensor对tensor求导,只允许scalar对tensor求导。
如果想对已经设置requires_grad=True的张量停止自动求导,有两种方式:
1.使用with torch.no_grad()包裹
2.使用.detach()获取一个新的不需导数的张量
print(x.requires_grad)
print((x**2).requires_grad)
with torch.no_grad():
print((x**2).requires_grad)
print(x.requires_grad)
y=x.detach()
print(y.requires_grad)
print(x.eq(y).all())
torch.nn用于构建神经网络。
现在你已经了解了autograd包,nn依赖autograd以定义模型并对其求差分。nn.Module的一个实例会包含网络层,以及一个forward(input)方法用于返回output。
如,看看下边这个定义用于对位图分类的网络:
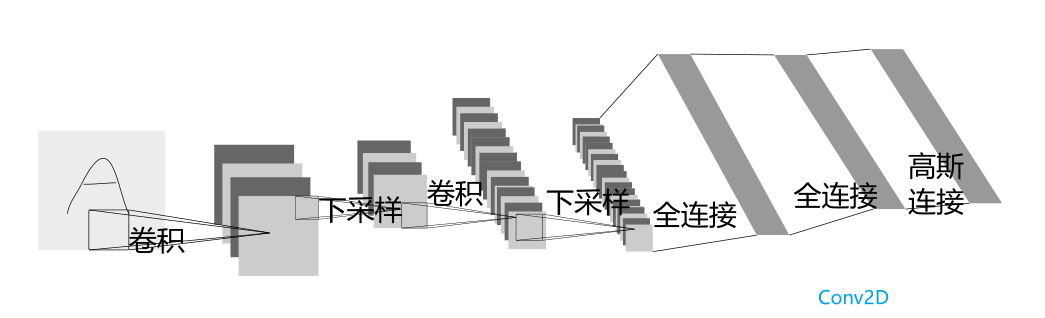
上图是一个简单的前向网络,它接收输入,依次喂给几层,最终得到输出。 一个典型的训练过程如下:
- 定义有一些可训练参数的网络
- 输入一组数据
- 前向传播
- 计算损失函数值
- 反向传播获取梯度
- 更新网络权重,通常使用
weight=weight-learning_rate*gradient
以下代码用于定义网络:
import torch
import torch.nn as nn
import torch.nn.functional as F
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
# 输入只有一个灰度channel,输出为6个channel,每个channel为3*3卷积获取
self.conv1 = nn.Conv2d(1,6,3)
self.conv2 = nn.Conv2d(6,16,3)
# 尾部的全连接层
# 3*3卷积得到的输出是6*6
self.fc1 = nn.Linear(16*6*6, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def num_flat_features(self, x):
size = x.size()[1:]
# batch维不会被压平
num_features = 1
for s in size:
num_features *= s
return num_features
def forward(self, x):
# 做最大池化以下采样
x = F.max_pool2d(F.relu(self.conv1(x)), (2,2))
# 如果是用的方阵的话也可以只写行数或列数
x = F.max_pool2d(F.relu(self.conv2(x)), 2)
# 形状变换
x = x.view(-1, self.num_flat_features(x))
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
net = Net()
print(net)
你必需定义forward方法。backward方法会在指定autograd时自动计算得到。forard方法中可以用任意tensor操作。
网络可学习的参数由net.parameters()导出:
params = list(net.parameters())
print(len(params))
print(params[0].size())
我们测试一个随机的32x32输入。注意这个网络的输入大小是32x32。为了在MNIST数据集上使用这个网络,必需将数据的大小变换为32x32:
input = torch.randn(1,1,32,32)
out = net(input)
print(out)
清空所有参数的梯度缓存,使用随机梯度进行反向传播:
net.zero_grad()
??torch.nn.Module.zero_grad
# 这里为何要用随机,不用ones呢
out.backward(torch.randn(1,10))
*注意
torch.nn只支持mini-batch,这意味着torch.nn包只支持以mini-batch形式输入的sample,不支持单个sample。
比如nn.Conv2d接受的是一个4D Tensor:
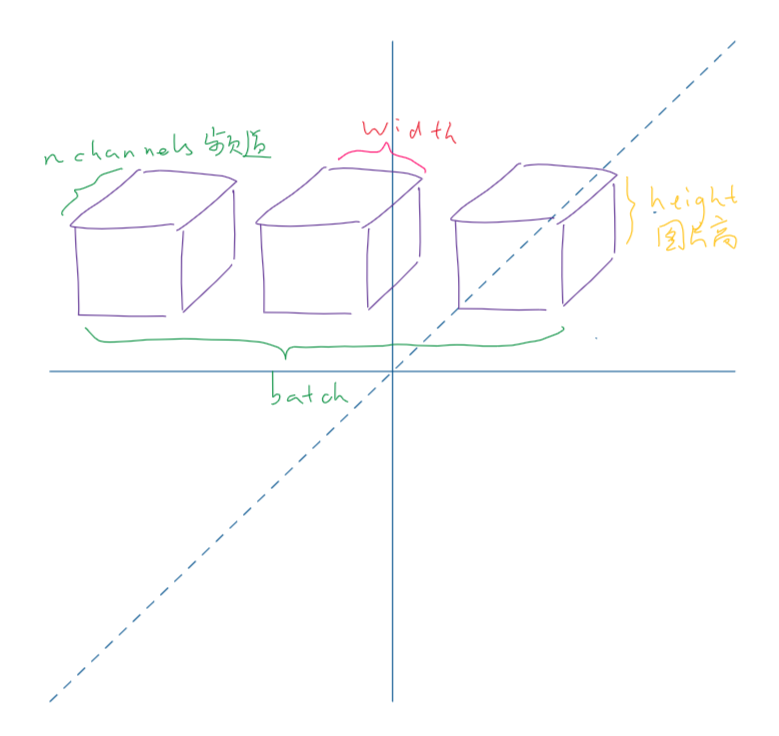
input.unsqueeze(0)添加一个假的batch维度。
*
在继续之前,先回顾一下我们见过的所有类: 回顾
*
torch.Tensor - 是一个支持backwrd()形式的自动差分操作的多维数组。他也持有梯度值;
-
nn.Module神经网络模块,方便打包模型参数以加载、导出或者迁移。 -
nn.Parameter在配置为Module的属性时,会被自动注册为模型参数。 -
autograd.Function每个Tensor操作创建至少一个Function节点,该节点与一个创建Tensor的方法相关联。
我们已经做的
- 定义一个神经网络
- 处理输入并反向传播
待做的
- 计算loss
- 更新网络权重
损失函数接受(输出,目标)格式输入,并计算出一个值,用于衡量输出与目标之间的偏离程度。
nn包提供了几种不同的损失函数。nn.MSELoss计算了输入与目标之间的均方误差。
比如:
output = net(input)
target = torch.randn(10)
target = target.view(1, -1)
criterion = nn.MSELoss()
loss = criterion(output, target)
print(loss)
现在,如果你用.grad_fn去跟随loss的反向传播过程,你会看到一个这样的计算图:
input -> conv2d -> relu -> maxpool2d -> conv2d -> relu -> maxpool2d
-> view -> linear -> relu -> linear -> relu -> linear
-> MSELoss
-> loss
所以当我们调用loss.backward()时,整个计算图对loss求梯度,图中设置require_grad=True的Tensor将把它们的.grad属性与梯度相加。
比如,我们回溯几步:
print(loss.grad_fn)
print(loss.grad_fn.next_functions[0][0])
print(loss.grad_fn.next_functions[0][0].next_functions[0][0])
为了反向传播误差,我们必须手动调用loss.backward()。调用之前需要清除已有的梯度值,否则会累加到已有的梯度值上。
现在我们需要调用loss.backward(),并分别在调用前和调用后查看convI的偏差值。
net.zero_grad()
print('conv1.bias.grad befor backward')
print(net.conv1.bias.grad)
loss.backward()
print('conv1.bias.grad after backward')
print(net.conv1.bias.grad)
现在,我们知道了如何应用损失函数。
需要学习的只有一个:
- 更新网络的权重。
最简单的权重更新规则是随机梯度下降(SGD),如下:
weight = weight - learning_rate * gradient
我们可以用简单的python代码实现该功能:
learning_rate = 0.01
for f in net.parameters():
f.data.sub_(f.grad.date * learning_rate)
但是,在你使用网络时,你可能想用不同的更新规则如Adam、RMSProp等。为了支持这些更新规则,我们创建了一个轻量包torch.optim以实现这些方法。使用非常简单:
import torch.optim as optim
# 创建优化器
optimizer = optim.SGD(net.parameters(), lr=0.01)
# 在训练的过程中
optimizer.zero_grad()
output = net(input)
loss = criterion(output, target)
loss.backward()
optimizer.step()
注意梯度缓存必须手动用optimizer.zero_grad()方式清除,这是因为梯度是一个累加值
你已经看到如何定义神经网络,计算损失并且更新网络的权重,现在你可能在思考。
通常,在你处理图像、文本、声音或影像数据时,你可以用标准的python包将数据读入一个numpy数组,此后你就可以将数组转为tensor:
- 图像方面,Pillow或OpenCV都有用
- 声音方面,scipy或者librosa都有用
- 文本方面,原始的python、cython、NLTK或者SpaCy都有用
特别的,对于视觉类任务,我们创建了一个名为torchvision的包,可以用于Imagenet,CIFAR10,MNIST等数据集的导入。 这使得我们得以避免重写一些数据载入的代码。
本教程中,我们将用 CIFAR 10数据集举例。该数据集包含10个类别,每个样本都是一个33232的多维数组:

我们将依次进行下列操作:
1.读取和正则化CIFAR 10 训练和测试集 2.定义一个CNN 3.定义一个损失函数 4.在训练集上完成训练 5.使用测试集完成测试
使用torchvision时,读取CIFAR10数据集非常简单:
import torch
import torchvision
import torchvision.transforms as transforms
torchvision的输出是[0,1]之间的PILImage格式图片。我们将它们转化为[-1,1]之间的数据。
如果你在windows上运行遇到BrokenPipeError,将torch.utils.data.DataLoader()的num_worker参数设置为0
import torch
import torchvision
import torchvision.transforms as transforms
transform = transforms.Compose(
[transforms.ToTensor(), transforms.Normalize((0.5,0.5,0.5),(0.5,0.5,0.5))])
trainset = torchvision.datasets.CIFAR10(root='../data', train=True,download=True,transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=4,shuffle=True, num_workers=2)
testset = torchvision.datasets.CIFAR10(root='../data', train=False, download=True, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=4, shuffle=False, num_workers=2)
classes = ('plane','car','bird','cat','deer','dog','frog','horse','ship','truck')
我们看几张训练集中的图片:
import matplotlib.pyplot as plt
import numpy as np
def imshow(img):
img = img/2 + 0.5
npimg = img.numpy()
plt.imshow(np.transpose(npimg, (1,2,0)))
plt.show()
dataiter = iter(trainloader)
images, labels = dataiter.next()
# 查看图片
imshow(torchvision.utils.make_grid(images))
# 打印类别
print(' '.join('%5s' % classes[labels[j]] for j in range(4)))
import torch
import torch.nn as nn
import torch.nn.functional as F
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
# 输入为3通道,输出为6个channel,每个channel为5*5卷积获取
self.conv1 = nn.Conv2d(3,6,5)
# ? 之前用nn.functional.max_pool2d即可,现在换成nn.MaxPool2d了
self.pool = nn.MaxPool2d(2,2)
self.conv2 = nn.Conv2d(6,16,5)
# 尾部的全连接层
# 5*5卷积得到的输出变小了
self.fc1 = nn.Linear(16*5*5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def num_flat_features(self, x):
size = x.size()[1:]
# batch维不会被压平
num_features = 1
for s in size:
num_features *= s
return num_features
def forward(self, x):
x = self.pool(F.relu(self.conv1(x)))
# 如果是用的方阵的话也可以只写行数或列数
x = self.pool(F.relu(self.conv2(x)))
# 形状变换
x = x.view(-1, 16 * 5 * 5)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
net = Net()
print(net)
我们用一个分类器交叉熵做为损失函数,并用带动量的SGD作为权重更新方法:
import torch.optim as optim
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)
开始变得好玩了,我们只需要遍历我们的数据迭代器,将输入喂给网络并进行优化:
for epoch in range(2):
running_loss = 0.0
for i, data in enumerate(trainloader, 0):
inputs, labels = data # 数据是一个序列
optimizer.zero_grad() # 清空梯度缓存
# 前向传播
outputs = net(inputs)
# 反向传播
loss = criterion(outputs, labels)
loss.backward()
# 更新权重
optimizer.step()
# 打印统计参数
running_loss += loss.item()
if i%2000 == 1999:
print('[%d, %5d] loss: %.3f' % (epoch + 1, i+1, running_loss / 2000))
running_loss = 0.0
print('Finished Training')
最后保存我们训练好的模型:
PATH = '../model/cifar_net.pth'
torch.save(net.state_dict(), PATH)
我们在训练集上训练了两个epoch,现在检查下网络是否有学到什么东西。
我们通过预测网络对于测试集的输出,并将其与ground-truth相互对比,如果预测结果正确,则将结果加入正确预测列表之内。
首先,看下测试集中的一个minibatch:
dataiter = iter(testloader)
images, labels = dataiter.next()
# 打印图片
imshow(torchvision.utils.make_grid(images))
print('GroundTruth:', ' '.join('%5s' % classes[labels[j]] for j in range(4)))
之后,我们加载已经读取的模型:
net = Net()
net.load_state_dict(torch.load(PATH))
现在我们看看网络认为上述示例是什么类型:
outputs = net(images)
输出的是10个类别的分数。某个类别的分数越高,网络就越是认为样本属于这个类别。因此我们获取具有最大分数的类别作为结果:
_, predicted = torch.max(outputs, 1)
print('Predicted: ', ' '.join('%5s' % classes[predicted[j]] for j in range(4)))
?错了一个,和原始教程中不一样。 我们再看看网络在整个数据集上的表现:
correct = 0
total = 0
with torch.no_grad():
for data in testloader:
images, labels = data
outputs = net(images)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
print('Accuracy of the network on the 10000 test images: %d %%' % (100*correct / total))
看起来比随机猜测好很多(随机猜测有10%的概率猜中,准确率的期望为 10%)。网络学到了一些东西。
我们看看在哪些类别上网络表现好,哪些差:
class_correct = list(0. for i in range(10))
class_total = list(0. for i in range(10))
with torch.no_grad():
for data in testloader:
image, labels = data
outputs = net(images)
_, predicted = torch.max(outputs, 1)
c = (predicted == labels).squeeze()
for i in range(4):
label = labels[i]
class_correct[label] += c[i].item()
class_total[label] += 1
for i in range(10):
print('Accuracy of %5s : %2d %%' % (classes[i], 100 * class_correct[i] / class_total[i]))
我们该如何在GPU上运行这些网络呢?
可以用和迁移Tensor一样的方法将网络迁移到GPU上。 首先设置设备为首个cuda设备,如果cuda可用的话:
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
print(device)
如若机器上有CUDA设备,那么这些方法将递归地遍历所有模块,并将它们的参数和缓存转换为cuda上的张量:
net.to(device)
同时,你也需要将每一步的输入和目标送个GPU:
inputs,labels = data[0].to(device), data[1].to(device)
为什么GPU速度没有明显提升呢?因为网络太小了。
练习增加网络的宽度(首个nn.Conv2d的第二个参数与第二个nn.Conv2d的第一个参数),看看加速能达到多少。
目标完成:
- 理解Tensor库和神经网络
- 训练一个小的神经网络用于分类图片